Concepto de similaridad y modelo de espacio vectorial

¿Cómo definimos la similaridad entre 2 cosas?

Es fácil decir que una persona se parece a otra, pero ¿con base en qué lo aseguramos? Color de piel, ojos, rasgos en común, tipo de peinado, forma de la cara, etc., son algunos de los factores que nos ayudan a decidir si una persona es similar a otra. Pero, ¿cómo llevamos esto a palabras?

Cuando decimos que una palabra “se parece” a otra, podemos enforcarnos en 2 aspectos: sintáctico y semántico. Por ello, necesitamos encontrar en cada caso factores que nos ayuden a determinar qué tan similares o diferentes son 2 palabras. Por el momento, aquí nos enfocaremos al aspecto sintáctico.

Uno de los métodos más usados para definir la similaridad entre palabras es la distancia de edición. Esto se define como el número mínimo de operaciones que hay que realizar en la primera palabra para convertirla en la segunda. El método más común es el denominado distancia de Levenshtein, en el que las operaciones aplicables a palabras son “insertar“, “borrar” y “sustituir“. Por ejemplo, la distancia de Levenshtein entre “perro” y “cerro” es 1, porque para obtener la segunda palabra a partir de la primera solamente necesitamos sustituír la “p” de la primera palabra por “c”. Entre “perro” y “caro” la distancia es 3, porque hay que cambiar la “p” por “c”, la “e”, por “a” y borrar una “r” para obtener la segunda palabra. Creo que la idea es clara, y varios seguramente se imaginarán ya que algo así es la base de los correctores ortográficos.

Ahora, veamos cómo definir la similitud entre algo menos concreto con un ejemplo muy simple. Supongamos que tenemos un negocio que sirve desayunos a estudiantes, pero en el menú solamente hay 2 platillos y una bebida: huevos, rebanadas de jamón y jugo de naranja. Un estudiante puede pedir su desayuno especificando cuántos huevos, cuántas rebanadas de jamón y cuantos vasos de jugo de naranja quiere. ¿Cómo podemos medir la similitud entre los desayunos de 2 estudiantes?

Podemos pensar que simplemente contando los ingredientes y el número de cada uno en cada desayuno puede darnos una métrica, pero ¿qué tan diferente es un desayuno de un huevo con una rebanada de jamón y uno de un huevo con 2 vasos de jugo de naranja? Necesitamos una medición que nos dé algo concreto, algo que podamos comparar. ¿Qué tal definir cada ingrediente como una coordenada, y el número de cada uno es la distancia del origen en cada una de ellas?

Definamos entonces nuestras variables: H, J y N. Cada desayuno se compone de unidades en cada una de estos 3 ingredientes, que serán nuestros ejes, y la coordenada que forman (H, J, N, equivalente a x, y, z) será el desayuno en cuestión. Así, si un estudiante ordenó 2 huevos y un vaso de jugo de naranja, su desayuno se representa como (2H, 0J, N), y si alguien pidió un huevo, 2 rebanadas de jamón y 2 vasos de jugo de naranja, su desayuno es (H, 2J, 2N). Y como éstas son coordenadas, vamos graficándolas a ver qué nos dan.

Bien! Con los desayunos representados de esta forma (2 puntos en un sistema de coordenadas, aunque aquí apeeeenas se alcanzan a ver) ahora es posible medir su similitud con algo que funcione para ello. Si definimos que la similaridad entre 2 desayunos es la distancia que hay entre ellos, podemos usar la distancia euclideana para obtenerla. Definamos a los desayunos como p y q. Entonces calculamos:

Para el caso concreto del ejemplo ilustrado, la distancia sería:

¡Un número concreto! Cuanto más pequeña sea la distancia entre 2 desayunos, más similares serán, y lo contrario también funciona. ¿Hasta aquí todo bien?

Es notorio que si alguien llega y pide 100 huevos, 20 rebanadas de jamón y 40 vasos de jugo de naranja, su distancia con respecto a alguno de los desayunos usados en el ejemplo anterior será muy grande, y por ende, concluiremos que el desayuno es muy diferente al de los demás. Si estamos contentos con esta métrica, no hay ningún problema y todo funciona, pero también podemos pensar que 2 desayunos son similares si contienen lo mismo, sin importar la cantidad de cada platillo. Después de todo, si alguien pide 2 huevos y un jugo, y otra persona pide 1 huevo y 2 jugos, lo que difiere es el número que acompaña a cada producto, pero no el contenido en sí. Si queremos medir la similaridad de esta forma, la distancia euclidiana no nos ayuda ya que se basa en la diferencia de las cantidades de cada eje. Necesitamos algo más.

Si ya tenemos los desayunos expresados en coordenadas, siendo cada una un eje, podemos ver esa coordenada como un vector que va desde el origen del sistema de coordenadas hasta el punto en cuestión. Cierto es que de esta forma también el vector de un desayuno que contenga una cantidad mayor de platillos será mucho más “largo”, es decir, estará más alejado del origen que otro que no contenga tanto, pero en ese caso, en vez de medir la distancia que hay entre los 2 puntos, existe una similaridad que se calcula usando los ángulos entre vectores: la similaridad de cosenos. Si pensamos detenidamente en los vectores que forma los desayunos, independientemente de las cantidades de los platillos, nos damos cuenta de que, en efecto, sus ángulos no difieren tanto.

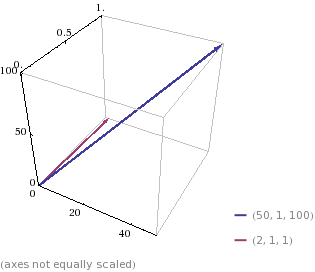
Usemos otros 2 desayunos como ejemplo; llamémoslos A y B.

A = 50 huevos, 1 rebanada de jamón, 100 vasos de jugo de naranja = (50H, 1J, 100N)

B = 2 huevos, 1 rebanada de jamón, 1 vaso de jugo de naranja = (2H, 1J, 1N)

Calculando la similaridad de cosenos:

Esto quiere decir que esos 2 desayunos se parecen, según este índice de similaridad, en un 73%. Si los desayunos fueran exactamente iguales, la similaridad de cosenos sería 1.

Y ahora…

Usando exactamente el mismo concepto, podemos calcular la similitud entre 2 documentos. El método es exactamente el mismo, con la única diferencia de que aquí vamos a trabajar en un plano de n dimensiones, donde n es el número de palabras únicas que existen en todos los documentos. En el ejemplo de los desayunos usé 3 ingredientes para poder visualizar lo que estaba pasando (3 ingredientes = 3 dimensiones), pero cuando se trabaja con documentos, hablamos de muchas, muchas dimensiones. Por fortuna, las matemáticas que se usan para hacer cálculos en ese tipo de estructuras ya existen. ¿Se acuerdan de sus clases de álgebra lineal? Si pensaban que lo que aprendieron ahí nunca lo usarían o no tenían usos en casos “reales” o en problemas “de verdad”, el manejo de documentos en lenguaje natural es un ejemplo que muestra lo contrario.

Esta forma de representar documentos usando vectores de los términos que contienen se conoce como “Modelo de espacio vectorial“. Con este modelo, ahora podemos enforcarnos en calcular la similaridad entre documentos y encontrar su relevancia con alguna consulta en específico, lo cual detallaré en la siguiente entrada de esta categoría.

* Todas las gráficas fueron creadas con Wolfram Alpha.