Implementando PageRank

Tuve oportunidad de leer este artículo técnico de Stanford, titulado “Searching the Web”:

 http://ilpubs.stanford.edu:8090/457/

Básicamente, es una explicación de cómo funcionan las búsquedas en internet; muestra lo que era el state-of-the-art en ese tópico, incluyendo el algoritmo que fue el comienzo de Google: PageRank.

Existen muchas páginas que describen en detalle cómo funciona esta técnica; incluso, el artículo mencionado arriba lo menciona de forma entendible, así que no ahondaré mucho en detalles: PageRank determina el grado de importancia de una página con base en el número de páginas que tienen ligas hacia ella. y del mismo grado de importancia de cada una de esas páginas. Es decir: una página será más relevante si muchas otras páginas ligan a ella, o también si las páginas que ligan a ella son a su vez relevantes.

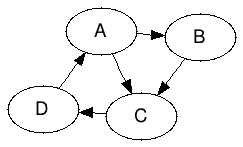
Consideremos el caso de una red que sólo tiene 4 sitios: A, B, C y D, y que están ligados de la siguiente forma:

Gracias a PageRank, podemos determinar la relevancia de cada uno de estos sitios, usando la fórmula que aparece en el artículo arriba mencionado:

(1)  

Donde r(i) es el pagerank de la página i, r(j) el pagerank de la página j, y N(j) es el número de links que salen de la página j. B(i) es el conjunto de páginas que tienen liga hacia la página i.

A ojo de buen cubero, la página C tendría un valor de relevancia mayor al de las otras páginas por haber 2 que ligan hacia ella (A y B).

Existen un par de problemas con esta fórmula: si encontramos una serie de páginas que sólo tienen ligas entre ellas, o si llegamos a una página que no tiene ligas a ningún lado, a final de cuentas la relevancia se centrará o en las páginas dentro de un cluster (para el primer caso) o convergerá a 0 (en el segundo caso). En el artículo, el primer caso se nombra como rank sink, mientras que el segundo se nombra rank leak.

Se propone también el modelo del Random Surfer para describir el comportamiento de un usuario: o bien puede seguir las ligas de una página a otra, o bien se puede aburrir y “brincar” directamente a una página.

Para resolver los problemas antes mencionados e implmentar al Random Surfer, lo siguiente es propuesto:

• Eliminar todas la páginas que no tengan ligas externas (leaks). No necesariamente la mejor solución.
• Suponer que los leak tienen ligas a todas las otras páginas.
• Agergar un valor que modele al Random Surfer. Este valor se denomina d (decay factor), y es un valor 0 < d < 1, indicando qué tan frecuentemente el Random Surfer se “aburre” de una página y brinca a otra aleatoriamente.

La fórmula anterior entonces cambia a:

(2)  

Donde d es el decay factor explicado arriba, m es el número total de páginas en la red, y el factor (1 – d) / m hace que la suma de todos los pagerank de las páginas consideradas sea igual a 1. Por supuesto, dependiendo del manejo de los sinks y leaks, los resultados varían.

Para información más detallada, consulten el artículo.

Power iteration

Es obvio pensar que teniendo tantas páginas que revisar necesitamos un método que sea lo más eficiente posible. Page y Brin mencionan que es posible hacer el cálculo de PageRank usando el método llamado Power Iteration, y que en un número relativamente bajo de iteraciones ( < 100 ) los valores convergen. Omito aquí la explicación técnica de obtener el principal eigenvector de la matriz de pagerank, y me centro específicamente en explicar el método con estructuras simples:

1. Inicializamos un vector s de longitud m = número de páginas. Cada valor es el pagerank de la página en cuestión. El valor inicial puede ser aleatorio, pero los autores lo inicializan en 1/m
2. Usando la fórmula (2), calculamos los nuevos valores de pagerank y los guardamos en un vector r.
3. Calculamos la L1 Norm de las diferencias absolutas entre r y s, y las comparamos con un valor de error máximo e previamente determinado. Si la L1 Norm es menor a e, los valores han convergido y r contiene los pagerank finales de las páginas. Si no, ir a 4.
4. Asignar a s los valores actuales de r y regresar 2.

Implementación

Como siempre, lo aquí establecido no es la verdad absoluta. Quienes estén interesados en mejorar la implementación o crear la suya propia, ¡adelante!

Cabe mencionar que lo aquí expuesto es sólo una parte de la implementación. Más abajo encontrarán la liga para revisar y descargar el código. Y por cierto, seguramente muchos esperarán que el código esté en Scala, pero para variarle (y no perder la práctica), lo hice en Java.

Lo primero que se me ocurrió fue usar un HashMap para encontrar rápidamente los valores que fuera necesitando, pero al mismo tiempo hacer el programa multithread, por lo que necesitaría sincronizar los métodos que accedieran al mapa, o bien definirlo concurrente usando un ConcurrentHashMap. A fin de cuentas, escogí lo segundo.

La idea era que las llaves del mapa fueran las páginas (String), y los valores fueran cualquier cosa que necesitara para hacer los cálculos, así como información que fuera relevante para la implementación. Por tanto, para los valores necesitaría una clase especial, a la que nombré como PRMatrixEntry, y a la clase que encapsularía el mapa la nombré como  PRMatrix.  Lo mínimo que necesitaba tener una PRMatrixEntry era:

• Una lista de los links que salen de la página.
• Una lista de las páginas que tienen ligas hacia esta página.
• El valor del pagerank para esta página.

Por ejemplo, usando el grafo de arriba, la entrada para la página A sería:

A → PRMatrixEntry(out = [B,C], in = [D], pagerank = 1/4)

Supuse  que crear una PRMatrix sería un proceso complicado, por lo que decidí ocultar el constructor y pasarle la responsabilidad de la creación del objeto a una Factory, a la que nombré PRMatrixFactory  (sip, yo súper creativo con los nombres :P).  Después de todo, las páginas se recibirán desde un archivo de texto; por tanto, la idea es pasarle a la Factory el nombre de archivo, dejar que la clase haga lo que tenga que hacer, y regrese el objeto que necesito.

Sinks y leaks

Encontrar leaks no es tan difícil con la estructura explicada: si una PRMatrixEntry no tiene ningúna página en las lista de ligas de salida, es un leak. Sin embargo, los sinks no son tan triviales de encontrar.

Pasé un rato tratando de encontrar una solución, pero no sabía exactamente qué buscar. Un sink puede estar conformado de muchas páginas… nada se me ocurría. Entonces, se me ocurrió buscar en teoría de grafos y encontré un algoritmo que me podía ayudar, Tarjan.

Lo que hace Tarjan es encontrar Strongly Connected Components (SCC), es decir, series de nodos que están conectados en un ciclo. De ahí pensé en aplicar Tarjan a las páginas, y después de tener los SCC, buscar en cada uno ligas a elementos fuera de ellos; si encuentro aunque sea una liga a una página fuera de los SCC, no es un sink.

Para darle flexibilidad al manejo de los leaks, decidí crear 2 estrategias y dar la opción de modificarlas por medio de un archivo de propiedades que se leerá al momento de iniciar el programa:

• Keep: Se agregarán al leak (también llamado dangling node) ligas a todas las otras páginas. Las estrategias de auto-ligas, explicadas abajo, también son tomadas en cuenta aquí.
• Ignore: No se agrega nada a los leaks. No contribuyen al cálculo del PageRank de las otras páginas.

Auto-ligas

No es difícil darse cuenta de que si una página tiene una liga a sí misma, afectará al valor de su PageRank y de las otras páginas a las que tenga ligas. Sin embargo, para darle flexibilidad a la implementación, aquí también decidí aplicar 2 estrategias, y dar la opción de modificarlas en el mismo archivo de propiedades mencionado arriba.

• Keep: Las auto-ligas serán agregadas y tomadas en cuenta.
• Ignore: Las auto-ligas serán ignoradas.

Las anteriores estrategias, tanto para leaks como para auto-ligas, afectan el cálculo del PageRank:

Consideremos el siguiente ejemplo, con 3 páginas (1,2,3):

1 2
2 1
2 3

3 es un rank leak.

Caso 1:
Auto-ligas: ignore
leaks: keep:
Resultados:

1 => 0.33321368565784804
2 => 0.428416335394704
3 => 0.2380128307091765

Caso 2:
Auto-ligas: keep
leaks: keep
Resultados:

1 => 0.3042573303760206
2 => 0.39117579750850107
3 => 0.3042573303760206

Caso 3:
leaks: ignore
auto-ligas: no importan
Resultados:

1 => 0.1372618008572723
2 => 0.17647610735248448
3 => 0.1372618008572723

Ligas duplicadas

Para tratar casos de ligas duplicadas (una página teniendo múltiples ligas a una misma página), simplemente convierto la lista de links de salida a un HashSet, que impide tener elementos duplicados.

Código

Como mencioné arriba, todavía hay muchos otros detalles que se explican mejor viendo directamente el código fuente.

Ciertamente poner todo el código aquí haría la entrada muy larga, por lo que cree un GitHub (¡al fin!) donde lo pueden encontrar y descargar:

https://github.com/medinamanuel/PageRank

El proyecto está “mavenizado”, por lo que les será fácil bajarlo y ejecutarlo. Están incluidos algunos archivos de prueba, muy simples. He probado el programa hasta con cerca de 2000 URLs y no he sentido impacto en el desempeño, pero está de más decir que todo tiene un límite (nada más falta encontrarlo, je).

Si puedo hacerme el tiempo, me gustaría implementar con Akka la parte multithread.

Un mini proyecto, de muchos que todavía tengo a medias :S