Para los que no están en contexto, spaCy es una librería de Python que provee funciones de PLN (procesamiento de lenguage natural, “NLP” en inglés) de una forma por demás fácil en comparación con, por ejemplo, NLTK.
Aunque conocía de su existencia, no había trabajado con spaCy hasta ahora que lo probé en el proyecto que tengo entre manos en el trabajo. Me era más familiar NLTK a pesar de haberlo usando en su mayoría en la versión 1 (van en la 3.5 al momento de escribir esto), pero para varias tareas spaCy es mucho más “directo”. Digamos que NLTK te da mucho poder, pero hay que ser mucho más específico al momento de manejarlo. En cambio, spaCy realiza muchas más acciones con menos interacción, lo cual puede ser bueno o extremo dependiendo del objetivo.
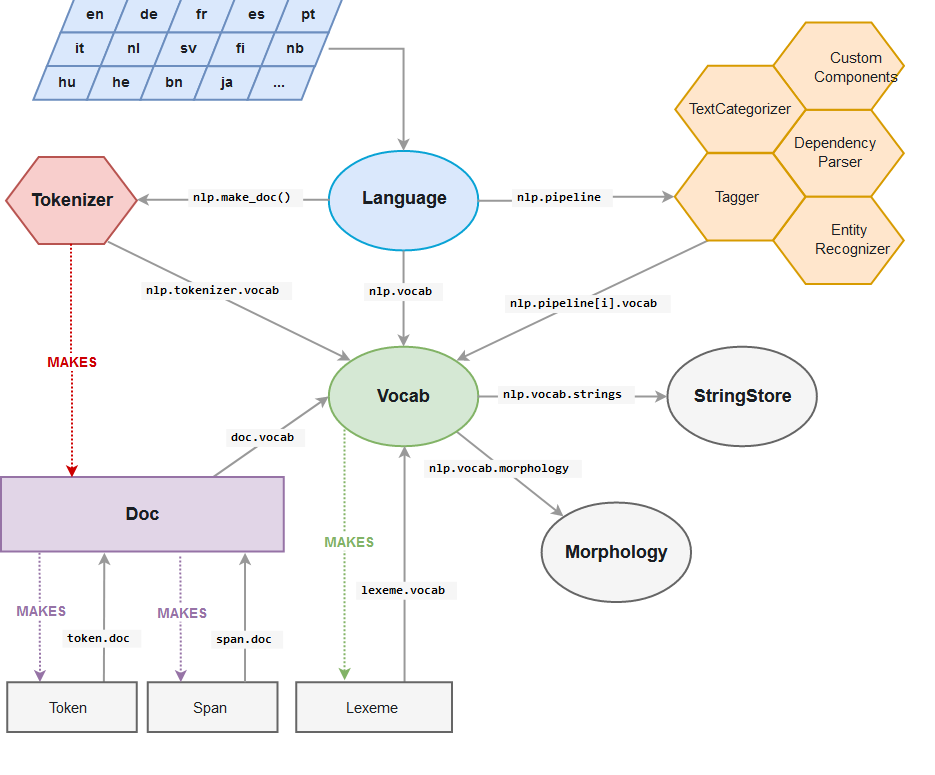 Lo interesante aquí para mí es nlp.pipeline. Una simple función, que por lo general la llaman nlp (pero uno puede definir el nombre), aplica una serie de algoritmos de análisis y reconocimiento, pero antes realiza el proceso de “tokenizar” el texto, es decir, dividirlo en entidades llamadas “tokens”, que son secuencias de caracteres agrupados en unidades semánticas. Es fácil irse con la finta de que todos los tokens son palabras, pero no es así. Existen además diferentes maneras de tokenizar, y dependiendo de la usada es el resultado que se tendrá. Por ejemplo, una de las maneras más fácil de tokenizar es agrupando caracteres en un texto separado por espacios, como este post, por ejemplo. Obviamente una tokenización así no serviría en idiomas como el japonés, donde las palabras no están separadas por espacios, pero ésa es otra historia. También es necesario destacar que separar por espacios tampoco es una forma ideal de tokenizar, incluso lenguajes como inglés, pero en sí no se puede dar una respuesta correcta sin saber cuál es el objetivo final. De eso depende la forma de crear tokens.
Lo interesante aquí para mí es nlp.pipeline. Una simple función, que por lo general la llaman nlp (pero uno puede definir el nombre), aplica una serie de algoritmos de análisis y reconocimiento, pero antes realiza el proceso de “tokenizar” el texto, es decir, dividirlo en entidades llamadas “tokens”, que son secuencias de caracteres agrupados en unidades semánticas. Es fácil irse con la finta de que todos los tokens son palabras, pero no es así. Existen además diferentes maneras de tokenizar, y dependiendo de la usada es el resultado que se tendrá. Por ejemplo, una de las maneras más fácil de tokenizar es agrupando caracteres en un texto separado por espacios, como este post, por ejemplo. Obviamente una tokenización así no serviría en idiomas como el japonés, donde las palabras no están separadas por espacios, pero ésa es otra historia. También es necesario destacar que separar por espacios tampoco es una forma ideal de tokenizar, incluso lenguajes como inglés, pero en sí no se puede dar una respuesta correcta sin saber cuál es el objetivo final. De eso depende la forma de crear tokens.
En el caso del análisis que estaba realizando (en inglés), requería manejar palabras como “well-known”, “state-of-the-art”, es decir, palabras compuestas por múltiples otras palabras, unidas por un guión (entre otros casos que no necesito nombrar), como un token. El problema es que el tokenizer de spaCy separa las palabras también por guiones, y estos a su vez forman tokens. Por ejemplo:
“well-known”
es tokenizado como
“well”, “-“, “known”
Cada elemento es un token, así que contiene más que el simple texto: su función gramatical, su forma base, entre otras cosas, todo gracias a que spaCy ejecuta las funciones de reconocimiento y análisis después de la tokenización, pero todo sucede dentro del mismo pipeline. Además, como cada token es identificado por separado, casos como el de “state-of-the-art” deben ser tratados ya que la palabra completa es un adjetivo, pero “art” por sí mismo es correctamente identificado como sustantivo. Algo se tiene que hacer.
Continue reading “Retokenizando con spaCy”