Day: April 15, 2014

Posted on

Implementando PageRank

Tuve oportunidad de leer este artículo técnico de Stanford, titulado “Searching the Web”:

 http://ilpubs.stanford.edu:8090/457/

Básicamente, es una explicación de cómo funcionan las búsquedas en internet; muestra lo que era el state-of-the-art en ese tópico, incluyendo el algoritmo que fue el comienzo de Google: PageRank.

Existen muchas páginas que describen en detalle cómo funciona esta técnica; incluso, el artículo mencionado arriba lo menciona de forma entendible, así que no ahondaré mucho en detalles: PageRank determina el grado de importancia de una página con base en el número de páginas que tienen ligas hacia ella. y del mismo grado de importancia de cada una de esas páginas. Es decir: una página será más relevante si muchas otras páginas ligan a ella, o también si las páginas que ligan a ella son a su vez relevantes.

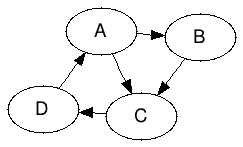
Consideremos el caso de una red que sólo tiene 4 sitios: A, B, C y D, y que están ligados de la siguiente forma:

pagerank-example1

Gracias a PageRank, podemos determinar la relevancia de cada uno de estos sitios, usando la fórmula que aparece en el artículo arriba mencionado:

(1)   \begin{equation*} r(i) = \sum_{j \epsilon B(i)} r(j) / N(j) \end{equation*}

Donde r(i) es el pagerank de la página i, r(j) el pagerank de la página j, y N(j) es el número de links que salen de la página j. B(i) es el conjunto de páginas que tienen liga hacia la página i.

A ojo de buen cubero, la página C tendría un valor de relevancia mayor al de las otras páginas por haber 2 que ligan hacia ella (A y B).

Existen un par de problemas con esta fórmula: si encontramos una serie de páginas que sólo tienen ligas entre ellas, o si llegamos a una página que no tiene ligas a ningún lado, a final de cuentas la relevancia se centrará o en las páginas dentro de un cluster (para el primer caso) o convergerá a 0 (en el segundo caso). En el artículo, el primer caso se nombra como rank sink, mientras que el segundo se nombra rank leak.

Se propone también el modelo del Random Surfer para describir el comportamiento de un usuario: o bien puede seguir las ligas de una página a otra, o bien se puede aburrir y “brincar” directamente a una página.

Para resolver los problemas antes mencionados e implmentar al Random Surfer, lo siguiente es propuesto:

  • Eliminar todas la páginas que no tengan ligas externas (leaks). No necesariamente la mejor solución.
  • Suponer que los leak tienen ligas a todas las otras páginas.
  • Agergar un valor que modele al Random Surfer. Este valor se denomina d (decay factor), y es un valor 0 < d < 1, indicando qué tan frecuentemente el Random Surfer se “aburre” de una página y brinca a otra aleatoriamente.

La fórmula anterior entonces cambia a:

(2)   \begin{equation*} r(i) = d * \sum_{j \epsilon B(i)} r(j) / N(j) + (1 - d) / m \end{equation*}

Donde d es el decay factor explicado arriba, m es el número total de páginas en la red, y el factor (1 – d) / m hace que la suma de todos los pagerank de las páginas consideradas sea igual a 1. Por supuesto, dependiendo del manejo de los sinks y leaks, los resultados varían.

Para información más detallada, consulten el artículo.

Power iteration

Es obvio pensar que teniendo tantas páginas que revisar necesitamos un método que sea lo más eficiente posible. Page y Brin mencionan que es posible hacer el cálculo de PageRank usando el método llamado Power Iteration, y que en un número relativamente bajo de iteraciones ( < 100 ) los valores convergen. Omito aquí la explicación técnica de obtener el principal eigenvector de la matriz de pagerank, y me centro específicamente en explicar el método con estructuras simples:

  1. Inicializamos un vector s de longitud m = número de páginas. Cada valor es el pagerank de la página en cuestión. El valor inicial puede ser aleatorio, pero los autores lo inicializan en 1/m
  2. Usando la fórmula (2), calculamos los nuevos valores de pagerank y los guardamos en un vector r.
  3. Calculamos la L1 Norm de las diferencias absolutas entre r y s, y las comparamos con un valor de error máximo e previamente determinado. Si la L1 Norm es menor a e, los valores han convergido y r contiene los pagerank finales de las páginas. Si no, ir a 4.
  4. Asignar a s los valores actuales de r y regresar 2.

Implementación

Como siempre, lo aquí establecido no es la verdad absoluta. Quienes estén interesados en mejorar la implementación o crear la suya propia, ¡adelante!
Continue reading “Implementando PageRank”